Algorithmic Overlap Estimations (Part 2)
Our hypotheses and assessments of the utility of several sketch data structures

This is the second of a 2-part post discussing some of the research behind our recently launched Datavant Trials. In Part 1, we discussed sketch data structures and our motivations for exploring them, and also outlined different approaches for computing overlap between datasets. Here, we offer our hypotheses about how each algorithm might perform on a variety of datasets, as well as our observations from testing.
Before undertaking our evaluation, we had some hypotheses about how the algorithms would perform.
Token Based Sampling (TBS v1 & v2)
Advantages
- Very simplistic
- Low-cost to implement and evaluate
Disadvantages
- Potentially an overly-naive approach that doesn’t actually serve as a good baseline
- Involves usage of additional cloud storage (to store quickly accessible subsets)
HyperLogLog (HLL)
Advantages
- One-time precomputing cost
- Directly supports dataset unions (combined data)
Disadvantages
- Typically doesn’t work well for <large:small> overlaps
- Appears to struggle if the true relative overlap is small (regardless of dataset sizes)
- Combinatorial time complexity for N-way intersections due to use of the Inclusion-Exclusion principle
HyperMinHash (HMH)
Advantages
- Same advantages as HLL
- Inclusion of MinHash may help in cases where there is a small true overlap
- Generally expected to outperform vanilla HLL in <large:small> overlaps
- Makes use of the pre-computed HLL values
- Linear time complexity for N-way intersections
Disadvantages
- Involves computing a MinHash which adds additional computational and storage overhead
Bloom filter – slow (BF-slow)
Advantages
- Generally expected to outperform HLL for <large:small> overlaps
- Allows for a straightforward implementation of N-way intersections (although not very efficient)
Disadvantages
- Smaller dataset in the overlap needs to be quite small for the estimation to run somewhat real-time
Bloom filter – fast (BF-fast)
Advantages
- Same advantages as HLL
- Easy to evaluate and control the false-positive rate to filter size tradeoff by adjusting various parameters
Disadvantages
- Requires that the bloom filters of the target datasets match in length
- Like HLL, makes use of the Inclusion-Exclusion principle, which makes generalizing to N-way intersections computationally intractable
Datasets used in our evaluation
Evaluating and comparing the estimation algorithms outlined in Part 1 of this post involved curating a diverse set of production datasets that could represent the range of overlap scenarios we’re interested in analyzing. We had previously simplified this as needing to compare <large:large>, <small:small>, and <small: large>, but in fact the results presented below are sourced from 55 unique overlap combinations between 11 datasets ranging from approximately 3K – 24M records and 3K – 7M individuals.
Evaluation Criteria
Our analysis of these algorithms aimed to address the following questions:
1. Are estimates < 20% for all size & true overlap scenarios?
To answer this, we evaluated all 55 combinations of datasets between the following two dimensions:
- sensitivity to the size discrepancy between datasets, quantified by the cardinality ratio between the smaller and the larger of overlapped datasets
- sensitivity to the ground-truth overlap between datasets, quantified by the relative size of the intersection (intersection cardinality as a fraction of the cardinality of the smaller of the two datasets) between the overlapped datasets
2. Do estimates bias towards overestimating or underestimating overlap amount?
To determine the performance of these algorithms on this metric, we plotted the overestimate to underestimate ratio (higher is better) against the mean percent error in estimating cardinality (lower is better) for each algorithm.
3. For a given dataset, are overlap estimates relatively consistent?
I.e. estimating that <A:B> has more overlap than <A:C> is still meaningful even if the absolute overlaps estimates aren’t accurate.
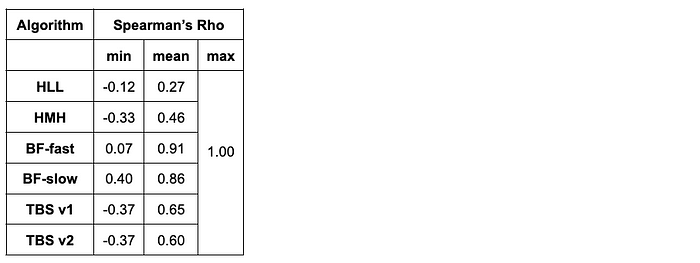
This question was answered by computing the mean Spearman’s Rho for each algorithm (averaging over the 11 unique datasets) by comparing the ground-truth ranking of datasets (from largest overlap to smallest overlap) with the predicted ranking generated from the estimated cardinalities.
Spearman’s Rho is a measure of rank correlation that ranges from -1 to 1 where:
- A value of 1 indicates a perfect match in ground-truth and predicted overlap rankings, and
- A value of -1 indicates a perfect mismatch (e.g. the ground-truth overlap ranking of query datasets against the target dataset E is [A, B, C, D] but the algorithm predicted the ranking as [D, C, B, A]).
Experiment results
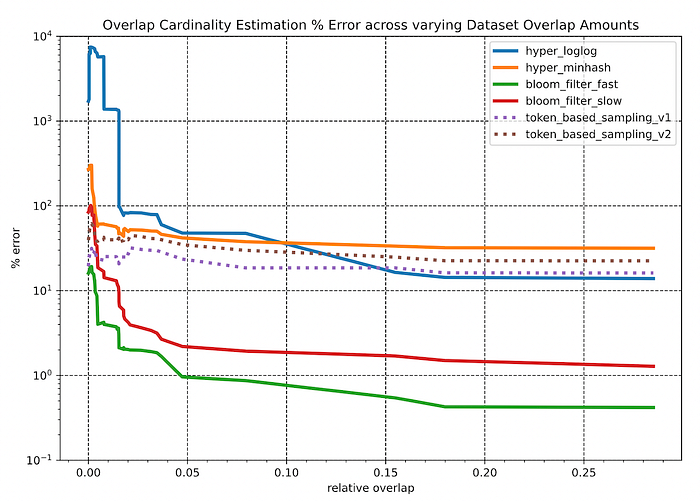
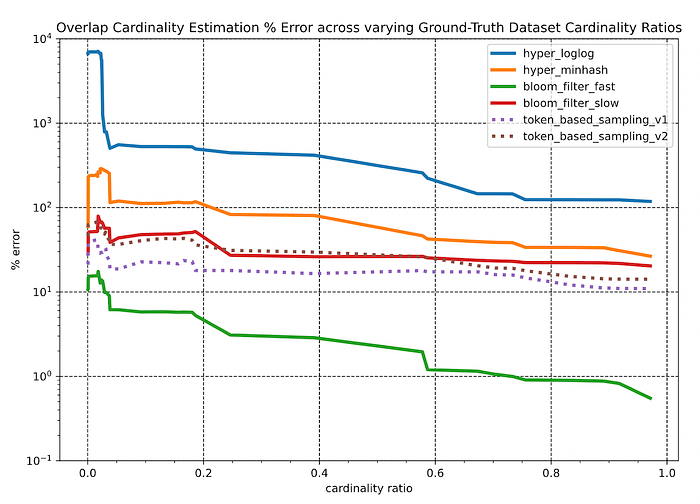
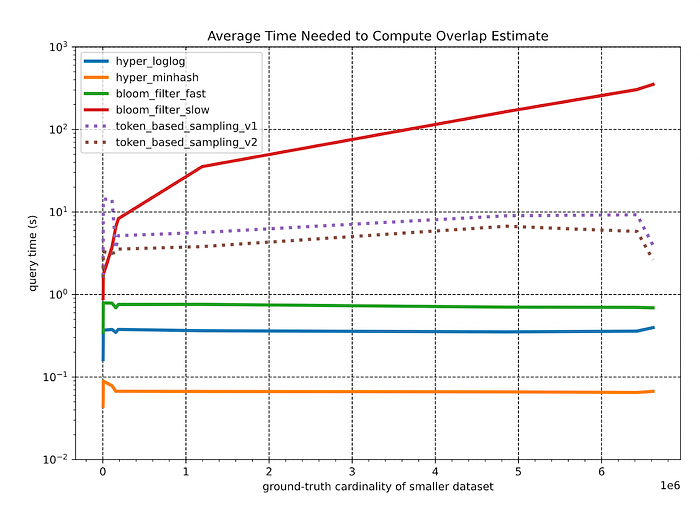
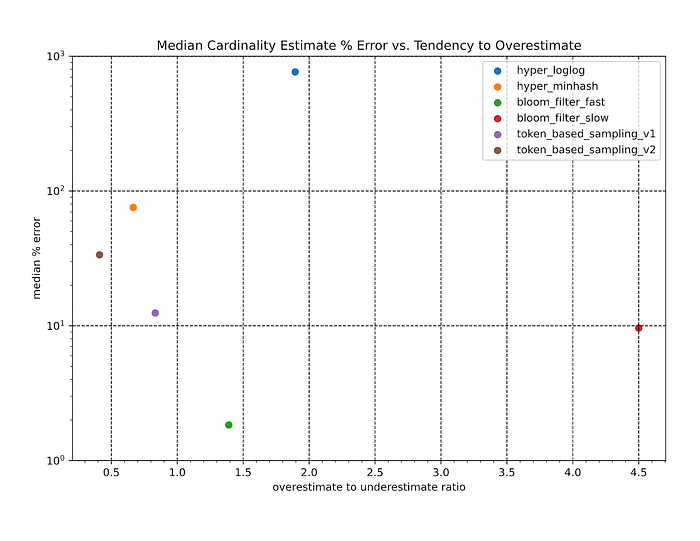
Key observations:
- Across the vast majority of overlapping scenarios, the Bloom-filter based approaches consistently outperform the other algorithms by 1 or more orders of magnitude.
- All sketching data structure-based algorithms seem to have a “breaking point” – at a relative overlap level below 5%, the estimation error skyrockets. However at this range, the relative error is less relevant. In a case where the ground-truth overlap between two datasets (~5M individuals overlapped against ~3K individuals) was merely 3, but the algorithm had predicted 5.7. The relative error is 98%, but the estimate is fairly good considering the absolute sizes of the two datasets.
- The sampling methods appear to be fairly insensitive to changes in both the relative overlap amount and the size ratios of the datasets. However, the overall performance of these methods falls short of the 20% error bound that would be needed for productionizing these solutions.
- As expected, all algorithms (apart from BF-slow) yield a relative constant query time for generating overlap estimates between arbitrary datasets since the underlying sizes of the sketch structures (or in the case of the sampling methods, the sample sets) are constant. Specifically, the fixed-size BFs used in the BF-fast approach prove to be consistently faster than the more complicated HLL and HMH sketches.
- The Bloom filter approaches additionally appear to produce more “stable” results by estimating the relative ranking of overlap amounts between a target dataset and a list of query datasets more correctly than the other algorithms. This was expected given the stark difference in estimation accuracy between these different algorithms.
Given our parameters here, the Bloom filter approaches are a clear winner among the approaches we tried. We continue to invest in making overlaps faster and more accurate, and part of a more streamlined user experience. If you’re interested in working on problems like this on large datasets, we are hiring for engineering roles at all levels.
REFERENCES
Algorithm Implementations/Libraries
We tested using the off-the-shelf implementations below.
BF-fast & TBS (v1 & v2) were implemented manually.
HLL: python-hll (Python)
HMH
- hyperminhash (Python)
- py-hyperminhash (Python)
- hyperminhash (GO)
BF: python-bloomfilter (Python)
See also:
https://schibsted.com/blog/1732486-2/
https://tech.nextroll.com/blog/data/2013/07/10/hll-minhash.html
https://towardsdatascience.com/big-data-with-sketchy-structures-part-2-hyperloglog-and-bloom-filters-73b1c4a2e6ad
https://en.wikipedia.org/wiki/Spearman%27s_rank_correlation_coefficient
Authored by
Abhijeet Jagdev, Aneesh Kulkarni and Nicholas DeMaison.
Considering joining the Datavant team? Check out our careers page and see us listed on the 2022 Forbes top startup employers in America. We’re currently hiring remotely across teams and would love to speak with any new potential Datavanters who are nice, smart, and get things done and want to build the future tools for securely connecting health data and improving patient outcomes.



